
Guest blogger Eric Linvill of Lightness by Design shares how composite materials modeling compares to solid modeling.
There are several ways to model multi-ply materials such as paperboard. Using a solid model with a thin domain for each layer is an obvious solution, but COMSOL also provides specific tools for modeling composite materials: the equivalent single layer (ESL) and layerwise theory (LWT) methods. Here, we will discuss these three different modeling methods and compare their model setups and results.
Multiple Methods to Model Layers
Composite materials technology is developed specifically for multi-ply material modeling, whereas for simple applications, a solid model could be sufficient. In addition to the details herein, there is an in-depth write-up of modeling paperboard formation with a solid model in a previous blog post.
The multi-ply nature of paperboard, however, lends itself nicely to composite modeling, which is why we focus here on the composite materials technology. The Composite Materials Module add-on to the COMSOL Multiphysics® software provides two methods for modeling multilayer materials that have additional benefits as compared to solid modeling: the equivalent single layer and layerwise theory methods.
Comparing the Equivalent Single Layer and Layerwise Theory Methods
Equivalent Single Layer Method
In this method, the elastic stiffness and rotational stiffness (i.e., bending stiffness) are homogenized onto a plane utilizing first-order shell theory for composites. The element type is a shell, meaning that each node (located on that plane) has six degrees of freedom in 3D: three translational degrees of freedom and three rotational degrees of freedom.
This method is computationally efficient for two reasons. First of all, ESL removes the thinnest part of the element geometry (i.e., the thickness), thus eliminating issues with poor element aspect ratios and allowing you to utilize a coarser mesh. Secondly, ESL removes some of the degrees of freedom through the thickness while doubling the degrees of freedom at each remaining in-plane node, which typically reduces the total number of degrees of freedom.
The simplifications of this theory imply that erroneous through-thickness stress and strain evaluations can be obtained, especially for nonlinear material responses (e.g., plasticity or hyperelasticity) and/or the assumption of a constant shear stress through the element during bending (which can be averted through the use of higher-order shell theory options).
Layerwise Theory Method
In this method, elements and integration points are constructed through the thickness and different plies of the shell. This means that only translational degrees of freedom are solved for at each node (i.e., three degrees of freedom in 3D). This provides more accurate through-thickness stress and strain results than the ESL method, at the cost of longer simulation times (due to a greater total number of degrees of freedom).
Unlike ESL, the LWT method is still sensitive to poor element aspect ratios because virtual nodes are utilized through the thickness of the model. In essence, the LWT method is just a solid element constructed from boundaries (2D geometries) and through-thickness ply data, which can drastically reduce model setup time as compared to a purely solid model. In addition, among many benefits, you have the freedom to choose different shape orders in the in-plane and out-of-plane directions in LWT, which is not possible in solid elements.
A visual representation of the nodes and elements for the two methods is shown in the following figure, where the reference surface can be the middle, top, or bottom of the actual volume (3D) or area (2D).
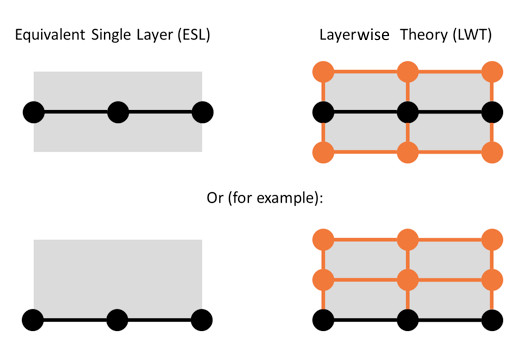
Nodes and elements for a 2D example of the ESL and LWT formulations in COMSOL Multiphysics. Black dots denote nodes that appear in the mesh visualized by COMSOL Multiphysics, orange dots denote virtual nodes that are utilized by COMSOL Multiphysics during the solution procedure and whose contribution appears in the total number of degrees of freedom, and the gray area denotes the spatial area of the layered structure.
Learn more about the COMSOL Multiphysics implementations of the ESL and LWT formulations in a previous blog post on the Composite Materials Module.
Now that we have outlined the composite materials technology, let’s compare the three different methods for modeling paperboard, or any other multi-ply material, in COMSOL Multiphysics: solid elements; the equivalent single layer method (i.e., shell elements with layered materials); and the layerwise theory method (i.e., layered shell elements).
Details of the Paperboard Model
The paperboard model is similar to the model in the previous paper mechanics blog post, but the middle ply measures 300 microns instead of 200 (the top and bottom plies are still 100 microns).
In order to benchmark these three models against each other, the mesh and shape functions need to be set in a consistent way across all three models. Note that, as previously mentioned, the equivalent single layer method allows you to utilize a coarser mesh while maintaining a good element aspect ratio, since the through-thickness geometry has been removed and replaced by a single surface. However, for benchmarking purposes, the mesh is controlled to be the exact same for all three models in-plane. A mesh element length of 1 mm is utilized in both x and y directions.
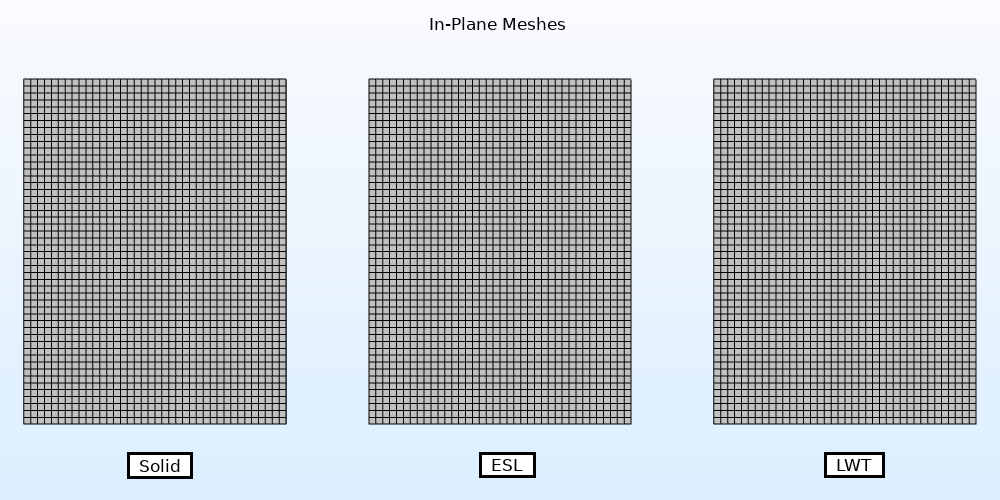
In-plane mesh of all three models, from left to right: solid, ESL, and LWT. All three meshes are identical.
The geometry and mesh for the out-of-plane direction is defined differently for the three models. The solid model is composed of three rectangular domains representing the three layers of folding box board (FBB), with five mesh elements. For the ESL model, the geometry is a boundary and only one element through the thickness is utilized. The LWT model also utilizes a boundary geometry, but five elements through the thickness are utilized and defined in the layered material table shown below.
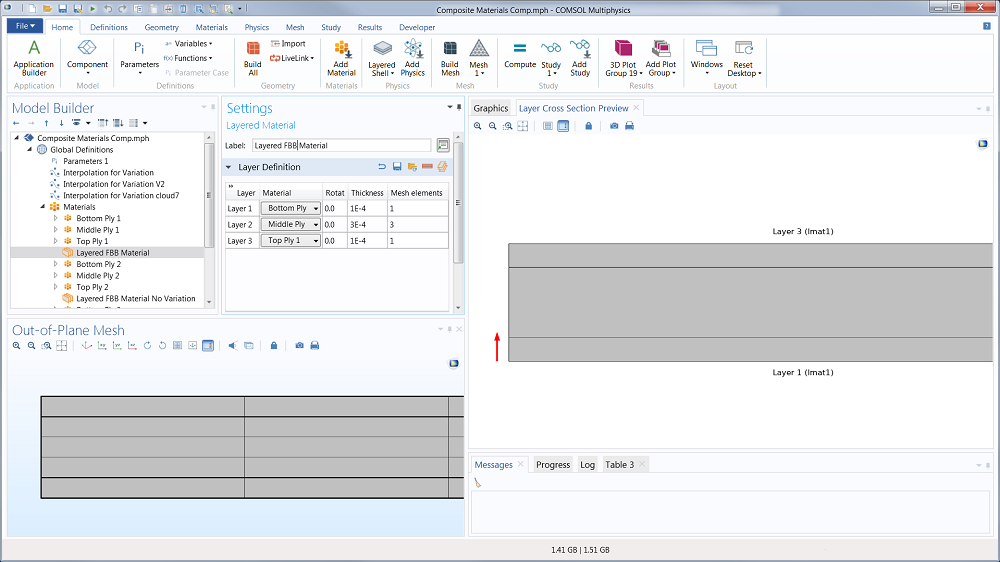
Out-of-plane mesh of the models with multiple elements through the thickness direction; the solid through-thickness mesh is shown in space (three domains and five mesh elements). The layers for the LWT model are shown in the Layered Material node under the global Materials node.
In addition to having consistent in-plane meshes, the models must have similar shape functions in order to make a side-by-side comparison. The Layered Shell formulation handles serendipity shape functions differently than the Solid formulation, so the shape functions for each model are set to quadratic Lagrangian. The solid and LWT models have five elements through the thickness. With quadratic shape functions, this means that the solid and LWT models have a total of 11 nodes through the thickness. The ESL model has only one node through the thickness (11 times less nodes than the solid and LWT models), but also has twice as many degrees of freedom per node and virtual node than the other models.
Therefore, for this specific example, the ESL model should have 2/11 (or 18.2%) the number of degrees of freedom as the solid and LWT models. The total number of degrees of freedom for the three models is shown in the following table, where the ESL model shows the exact ratio of 2/11 as compared to the solid model. Fewer degrees of freedom typically indicates shorter simulation times. The ESL model is also beneficial because you can use coarser meshes. However, for the sake of direct comparison, we’ll use the same mesh size for each model.
| Model | Degrees of Freedom (DOF) | DOF/(Solid DOF) |
|---|---|---|
| Solid | 256,641 | 100.0% |
| Equivalent single layer (ESL) | 46,662 | 18.2% |
| Layerwise Theory (LWT) | 256,641 | 100.0% |
Degrees of freedom for all three models as well as each model’s degrees of freedom divided by the degrees of freedom for the solid model.
These models use the same material properties and spatial material variation parameters as in the previous blog post. The spatial variability of the cross direction (CD) elastic modulus for all three models, all of which refer to the same spatial material variability field (i.e., all three models are subjected to the exact same material variability) is shown in the following figure. Note that the elastic moduli for the ESL and LWT models is plotted with the special plot tool Layered Material Slice.
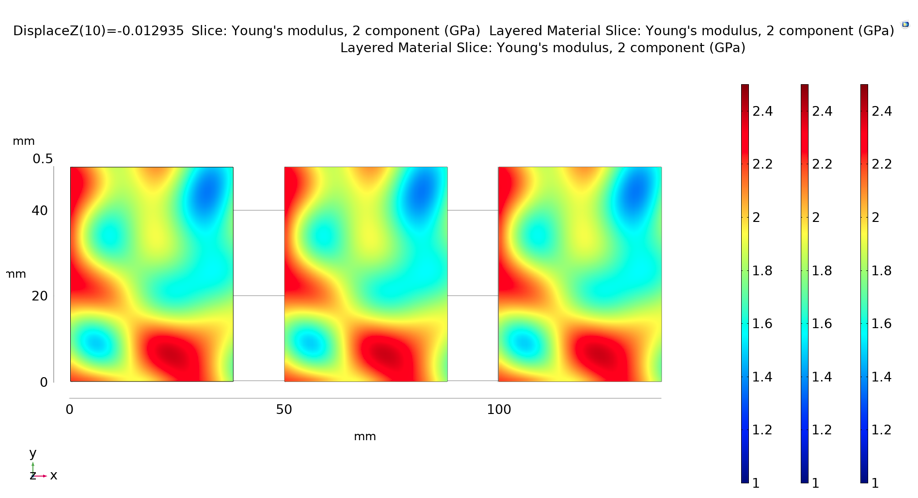
Elastic modulus in the CD for all three models. From left to right: solid, ESL, and LWT.
The paperboard is fixed in one end (at y = 0) and an out-of-plane (z) displacement is applied at the other end (at y = 50 mm), which corresponds to the 15° bending rotation during the Lorentzen & Wettre (L&W) bending test (explained further in part 1. Ten load steps are utilized to come to a solution.
Results and Discussion
The bending forces that provide a 15° bending rotation are provided in the following table. The resulting stress and strain fields during deformation are asymmetric, because the material properties themselves are asymmetric (as shown in the previous figure). The CD stress fields for the three methods are shown in the following figure. As is visible in the following table and figure, all three models give very similar results.
| Model | Bending Force (mN) |
|---|---|
| Solid | 247.7 |
| Equivalent single layer (ESL) | 248.5 |
| Layerwise theory (LWT) | 250.3 |
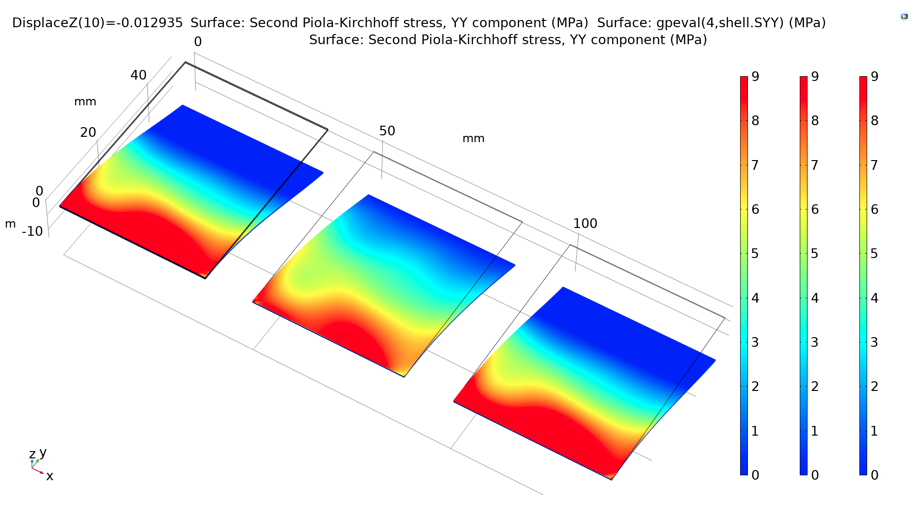
Stress field in CD on the upper surface of the paperboard. From left to right: solid, ESL, and LWT.
The solution times for the three different models are provided in the following table. Even though the ESL model has 18% the number of degrees of freedom as compared to the solid model, the solution takes only about 27% of the time that the solid model takes. This loss in performance is due to the fact that the ESL model requires the solution of additional equations (e.g., the homogenization of the layers into elastic stiffness, bending stiffness, and constant shear utilizing first-order shell theory for composites) that are not required for the solid model.
The LWT model takes a bit more time than the solid model. A majority of this extra solution time goes toward the extra steps that are required for the assembly of the stiffness matrix, especially regarding the interpolation of the material variations to each Gauss point. Regardless of the increased simulation time, the LWT model still has a total time advantage over the solid model. The geometry for the LWT model is only one boundary, whereas the geometry for the solid model is three domains and thus takes significantly more time to both create and apply the correct meshing parameters. Therefore, utilizing the LWT model still saves the most time (from conception to results) as compared to the solid model.
| Model | Solution Time (s) | Sol. Time/(Solid Sol. Time) |
|---|---|---|
| Solid | 152 | 100% |
| Equivalent single layer (ESL) | 41 | 27% |
| Layerwise theory (LWT) | 231 | 152% |
Solution time for all three models. Note that the total modeling time (including geometry creation, mesh settings, and solution) for the ESL and LWT models is quicker than for the solid model due to their inherent ease of use.
Conclusion
All three models successfully produce bending test results for the same materials and material variations. Using the solid model as the baseline, the ESL model provides a slightly quicker solution without accurate through-thickness results (not shown here). As compared to the solid model, the LWT model provides the exact same stress and strain results with significantly reduced modeling time and slightly increased computation time. This increase in computation time for the LWT model is attributed to the extra time that this model requires to assemble the stiffness matrix.
In addition to modeling multi-ply structures, the ESL and LWT models allow the following capabilities that are more difficult, or impossible, with the solid model:
- The constitutive behaviors of the interfaces between the layers can be included (but not post-peak delamination behavior, which need separate cohesive elements)
- Joints (e.g., corners of a box) can easily be modeled as rigid (constant angle), but flexible joints (joints with changing angle) cannot
- For complex geometries, generating a surface geometry is sometimes much easier than trying to make solid geometries, which could mean significant time savings in the modeling phase for complex geometries
Regardless, all three models are capable of handling linear elastic models of paper materials and other multi-ply materials, including spatial material variations.
Editor’s note, 3/21/23: The corresponding model files have been added to the Application Exchange. You can find the entry here.
Lightness by Design, a COMSOL Certified Consultant, offers simulation development and execution capabilities for advanced problems in paper mechanics as well as expertise with composite structures.
About the Author
Eric is a consultant at Lightness by Design, a COMSOL Certified Consultant, where he has a particular interest in paper-based packaging and aerospace structures. While these may seem like a random duo, the common links between these two applications are the utilization of lightweight load-bearing structures as well as fiber-based materials. Eric’s background in aerospace structural engineering includes both project experience as a consultant and formal BS education at Embry-Riddle Aeronautical University. After initial education in aerospace, Eric entered the exciting world of paper by pursuing a PhD in solid mechanics with a focus on paper mechanics at the KTH Royal Institute of Technology in Stockholm, Sweden, followed by 1.5 years in the R&D of the paper company WestRock. He has since been a consultant at Lightness by Design, where, in addition to consulting, he continues to develop FEM simulation tools (comprehensive user-defined materials and a virtual lab) that allow for advanced simulation of paper products and processes.






Comments (2)
Ulrik Skov
April 2, 2019Hi Eric,
Can you illustrated the:
– cross-section meshes and
– plot strains/stresses
inside the ply?
Kind Regards,
Ulrik
Eric Linvill
April 3, 2019Hi Ulrik,
Thanks for your question and your interest in my blog post! The cross-section meshes are actually illustrated in the above blog in the figure with the caption “Out-of-plane mesh of the models with…”. The following cross-section (i.e. out-of-plane) meshes are shown in that figure:
1) A close-up of the cross-section of the solid model is shown in the bottom left where one can see five elements through the thickness (vertical) direction.
2) A close-up of the non-meshed cross-section of the LWT model is shown in the right with the break-down of elements according to the table in the top left part of the figure (elements are equally spaced within each ply). The LWT is based on a Boundary (i.e. 2-D) geometry, so COMSOL therefore does not visualize the through-thickness mesh. In other words, this through-thickness mesh is handled internally but not visually.
3) The ESL model has no thickness and therefore no cross-section mesh. See the first figure in this post for example.
I assume you are interested in how strains and stresses through the thickness are affected by the different formulations. Such a comparison is done in very good detail with the Application Gallery example “Bending of a Simply Supported Composite Laminate” and I reference you there for a thorough comparison of through-thickness stress and strain results for ESL and LWT models against the theoretical result:
https://www.comsol.com/model/bending-of-a-simply-supported-composite-laminate-67641
Cheers,
Eric