Pressure Acoustics
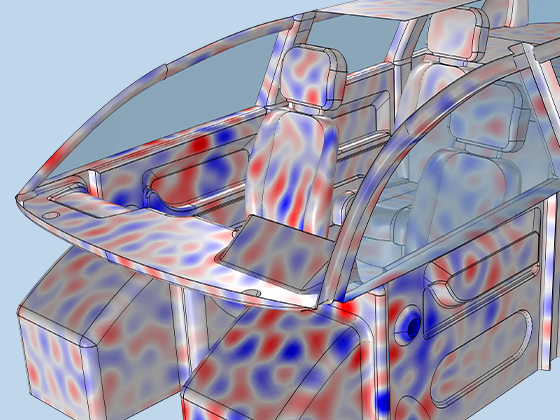
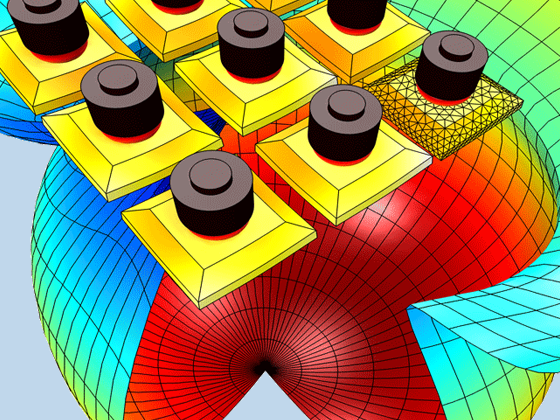
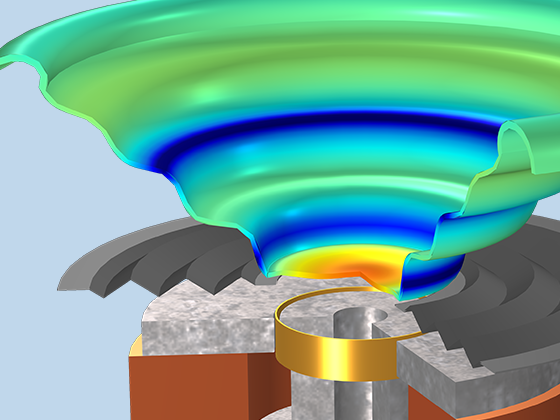
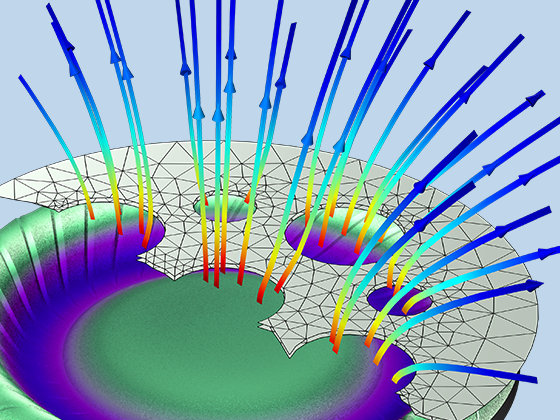
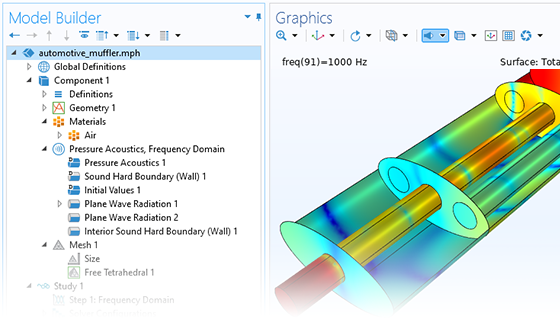
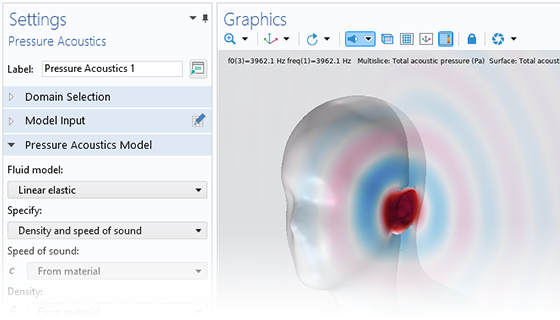
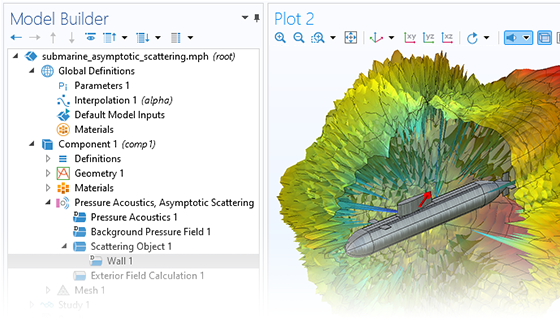
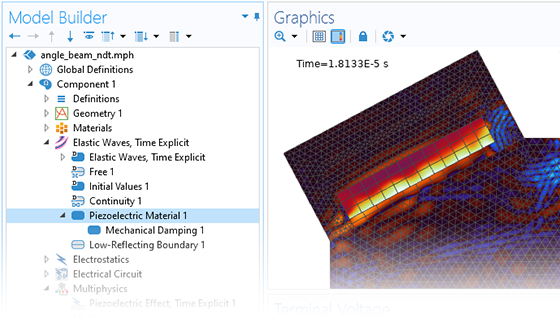
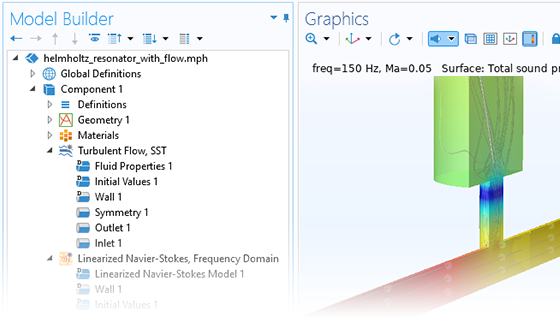
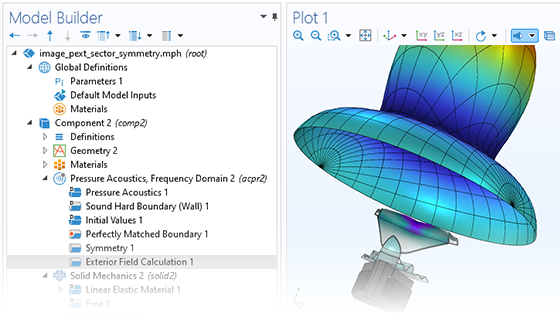
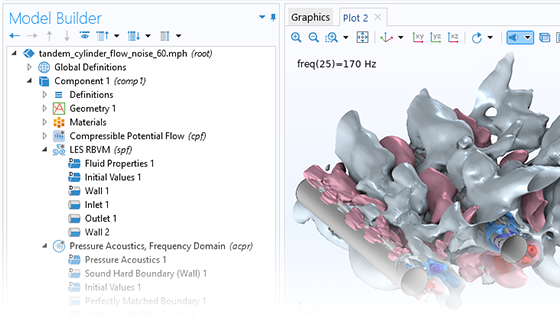
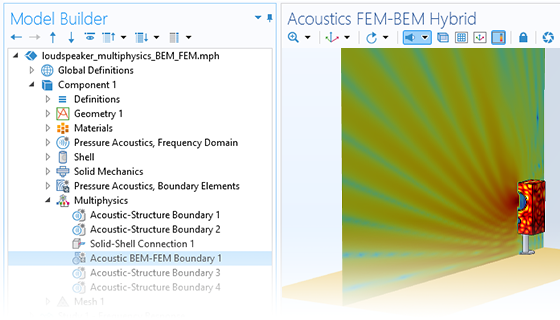
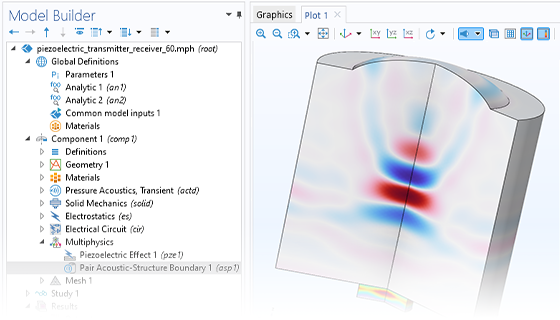
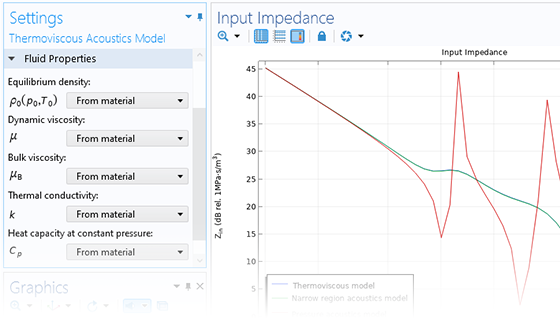
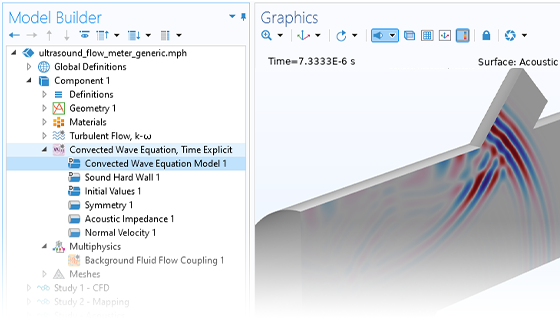
Pressure acoustics is the most common use of the Acoustics Module. You can model pressure acoustics effects, such as the scattering, diffraction, emission, radiation, and transmission of sound. Simulations run in the frequency domain employ the Helmholtz equation, whereas in the time domain, the classical scalar wave equation is used. In the frequency domain, both FEM and BEM are available, as well as hybrid FEM–BEM. In the time domain, time implicit (FEM) as well as time explicit (dG-FEM) formulations are available.
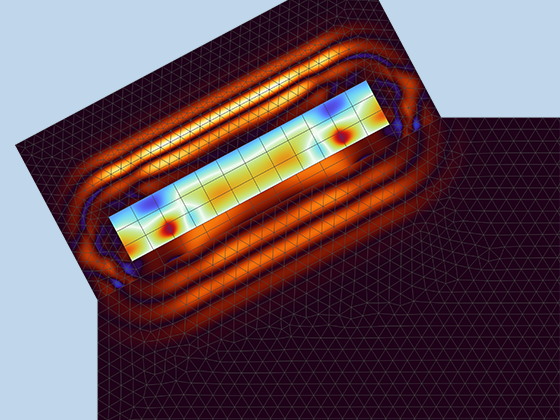
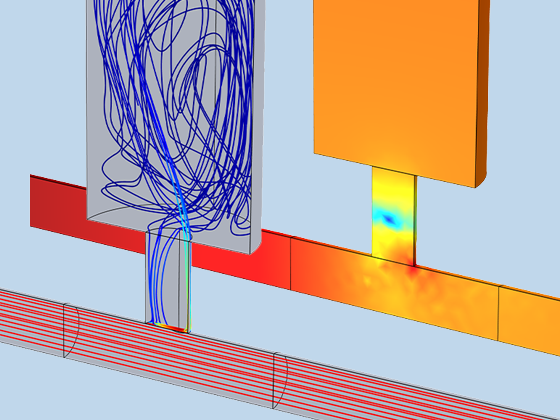
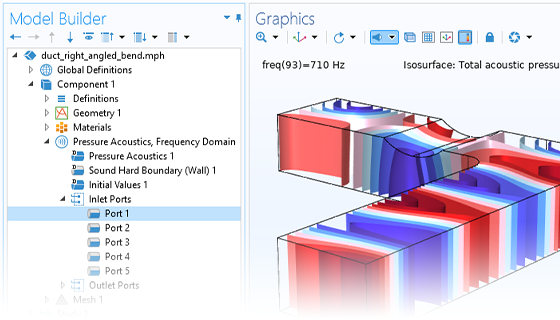
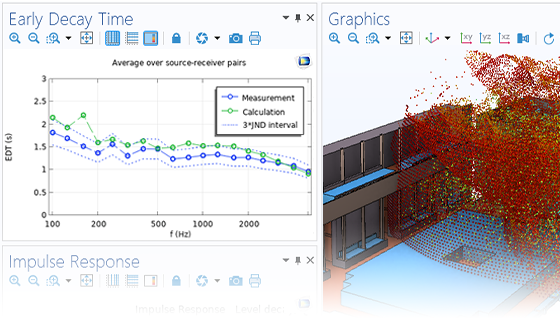
There are many options to account for boundaries in acoustics models. For instance, you can add a boundary condition for a wall or an impedance condition for a porous layer. You can use ports to excite or absorb acoustic waves at the inlet and outlet of waveguides using multimode expansion. Sources like prescribed acceleration, velocity, displacement, or pressure can be applied on exterior or interior boundaries. Further, you are able to use radiation or Floquet periodic boundary conditions to model open or periodic boundaries.
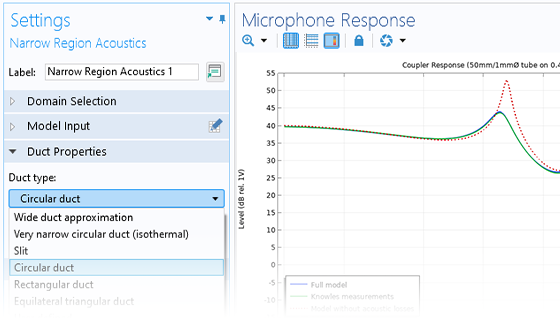
The Acoustics Module can also be used to model pipe acoustics, computing the acoustic pressure and velocity in flexible pipe systems. Applications include HVAC systems, large piping systems, and musical instruments such as organ pipes.