
Here, we begin an overview of the algorithms used for solving nonlinear static finite element problems. This information is presented in the context of a very simple 1D finite element problem, and builds upon our previous entry on Solving Linear Static Finite Element Models.
Editor’s note: The information in this blog post is superseded by this Knowledge Base entry: “Improving Convergence of Nonlinear Stationary Models”
A System of a Spring Attached to a Rigid Wall
Consider the system shown below, of a spring that is attached to a rigid wall at one end, and with an applied force at the other end. The stiffness of the spring is a function of the distance it is stretched, k(u)=exp(u). That is, the spring stiffness increases exponentially as it is stretched.
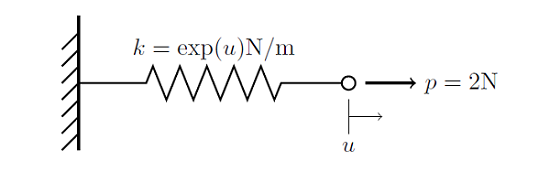
We are interested in finding the displacement of the end of the spring, where the force is applied. Just as we did earlier for the linear problem, we can now write the following function describing the balance of forces on the node for the nonlinear finite element problem:
In this case, only the spring stiffness is dependent on the solution, but more generally, both the load and the properties of the elements can be arbitrarily dependent upon the solution in a nonlinear problem.
Let us plot out this function, and keep in mind that we are trying to find u such that f(u)=0.
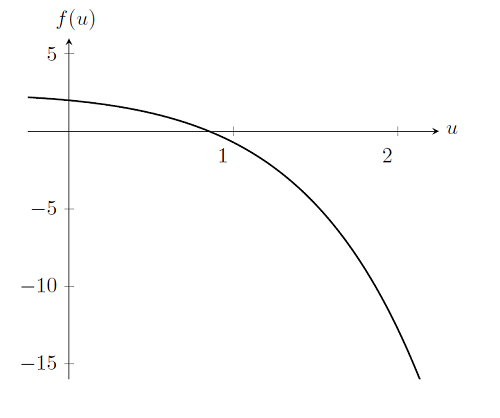
Finding the solution to the problem is, in fact, only marginally different from the linear case. Recall that to solve the linear problem we took a single Newton-Raphson iteration — and we do the exact same thing here:
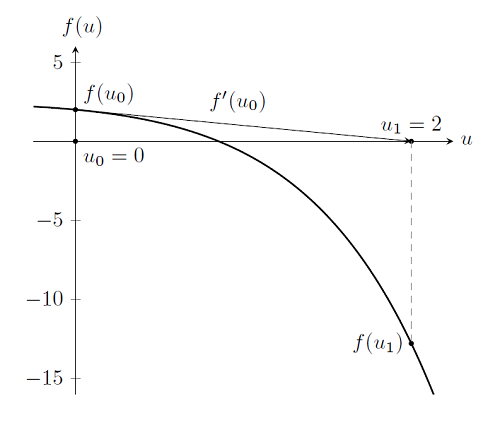
As you can see, we again start at an initial guess to the solution, u_0=0, and evaluate the function, f(u_0), as well as its derivative, f'(u_0). This gets us to the the point u_1. By examination, we see that this is not the solution, since f(u_1) \ne 0. But if we continue to take Newton-Raphson iterations, as shown below, it becomes clear that we are approaching the solution to the problem. (For more details about this algorithm, you can use this resource on Newton’s method.)
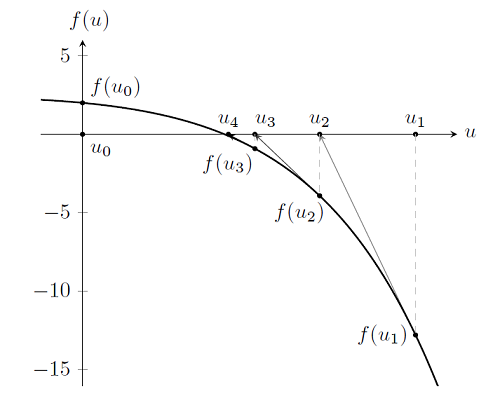
So finding the solution to a nonlinear problem is essentially identical to solving a linear problem, except that we take multiple Newton-Raphson steps to get to the solution. In fact, we could continue to take iterations and get arbitrarily close to the solution, but this is not needed. As discussed earlier, we always run into issues of numerical precision on computers, so there is a practical limit to how close we can get. Let’s have a look at the results after several iterations:
| i | u_i | |f(u_i)| | |u_{i-1}-u_i| | |f(u_{i-1})-f(u_i)| |
|---|---|---|---|---|
| 0 | 0.000 | 2.000 | ||
| 1 | 2.000 | 12.77 | 2.000 | 10.77 |
| 2 | 1.424 | 3.915 | 0.576 | 8.855 |
| 3 | 1.035 | 0.914 | 0.389 | 3.001 |
| 4 | 0.876 | 0.104 | 0.159 | 0.810 |
| 5 | 0.853 | 0.002 | 0.023 | 0.102 |
| 6 | 0.852 | 0.001 | 0.001 | 0.001 |
After six iterations, we see here that the difference between successive values of f(u), and u, as well as the absolute value of f(u), is reduced to 0.001 or less. After six Newton-Raphson iterations starting from u_0=0, the solution has converged to within a tolerance of 0.001. When we solve nonlinear problems, we apply this algorithm until the solution was converged to within the desired tolerance. There is a second termination criterion: that the solver should take no more than a specified number of iterations. Whichever criterion, tolerance, or number of iterations gets satisfied first will stop the solver. Also, keep in mind the discussion from the blog post on solving linear static finite element problems about the numerical scaling of the problem. The tolerance criteria applies to the scaled solution vector — not the absolute values of the solution.
Although it is more complicated to visualize, this is the same algorithm used to solve problems where u is a vector, as is the case for typical nonlinear finite element problems. However, when solving a problem with hundreds, thousands, or even millions of degrees of freedom, it is desirable to take as few Newton-Raphson steps as possible. Recall that we need to solve \mathbf{u}_{i+1}=\mathbf{u}_{i}-[\mathbf{f}'(\mathbf{u}_{i})]^{-1}\mathbf{f}(\mathbf{u}_{i}) and that computing the inverse of the derivative is the most computationally intensive step. To avoid proceeding into a region where there is no solution, and to minimize the number of Newton-Raphson steps taken, COMSOL uses a damping factor. Consider again the first Newton-Raphson step plotted earlier, and observe that for this step |\mathbf{f}(\mathbf{u}_{i+1})|>|\mathbf{f}(\mathbf{u}_{i})|. So for this iteration, we have taken too large of a step. When this happens, COMSOL will perform a simple search along the interval [\mathbf{u}_{i},\mathbf{u}_{i+1}] for a point \mathbf{u}_{damped}=\mathbf{u}_i+\alpha(\mathbf{u}_{i+1}-\mathbf{u}_i) such that |\mathbf{f(u}_{damped})|<|\mathbf{f(u}_{i})|. The Newton-Raphson iteration scheme is then restarted at this point.
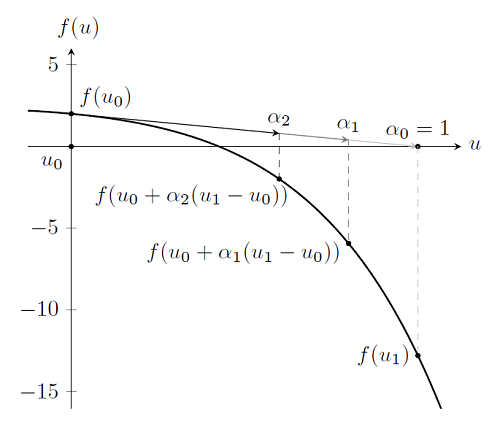
The term \alpha is known as the damping factor and has bounds 0< \alpha \le 1. As \alpha \rightarrow 0 we say that the damping is increased, while \alpha = 1 means that the problem is undamped. This method is attractive because the search requires only that COMSOL evaluates \mathbf{f(u}_{damped}) and the computational cost of this is quite low as compared to computing the derivative \mathbf{f'(u}_{i}) and its inverse [\mathbf{f}'(\mathbf{u}_i)]^\mathbf{-1}.
It is important to emphasize that this damping term has no direct physical interpretation. Although this method works quite well to improve convergence, there is very little physical insight that can be gleaned by examining the damping factor. Furthermore, although COMSOL does allow you to manually modify the damping factor, it is not generally possible to use any physical understanding or information from the model as guidance when doing so. The default choice of damping algorithm is difficult to outperform through manual intervention. However, there are other techniques that can be used, which are usually motivated by the physics of the problem, that work well when the default damped Newton-Raphson methods converge slowly or not at all.
Why Nonlinear Problems May Not Converge
Nonlinear problems are inherently difficult to solve since there are multiple ways in which the above solution procedure can fail to converge. Although there are many ways in which the Newton-Raphson method can fail, in practice we can reduce the discussion to the following cases.
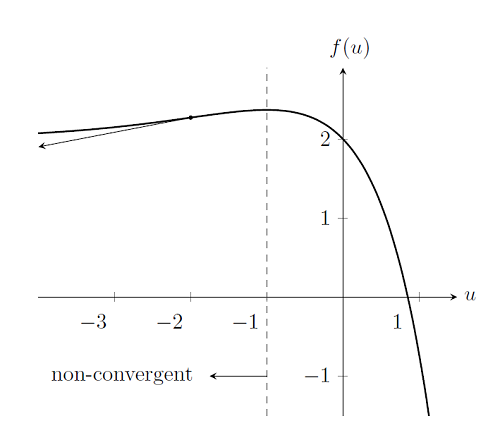
Case 1: The Initial Condition is Too Far Away from the Solution
First, consider the same nonlinear problem as before, but with a different starting point, for example, u_0=-2. As we can see from the plot below, if we choose any initial condition u_0\le-1, the Newton-Raphson method cannot find a solution since the derivatives of f(u) do not point towards the solution. There is no solution to be found to the left of u_0=-1, so these starting points are outside of the radius of convergence of the Newton-Raphson method. The choice of initial condition can cause the Newton-Raphson method to fail to converge, even if a solution exists. So, unlike the linear case, where a well-posed problem will always solve, the convergence of nonlinear models may be highly dependent on the choice of starting condition. We will address later how best to choose a good initial condition.
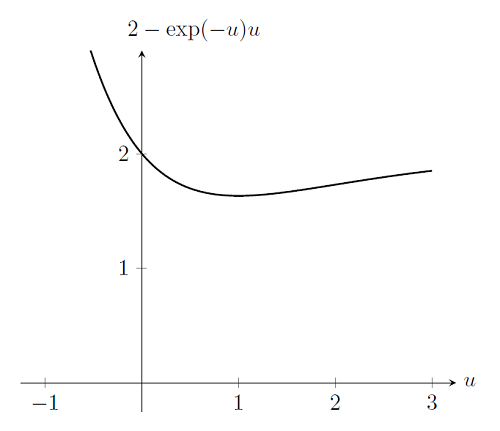
Case 2: The Problem Does Not Have a Solution
The nonlinear solver will also fail if the problem itself does not have a solution. Consider again the problem from above, but with a spring stiffness of k(u)=\exp(-u). In other words, as the spring gets stretched, the stiffness decreases. If we plot out f(u) for a load of p=2, we see that there is no solution to be found. Unfortunately, the Newton-Raphson algorithm cannot determine that this is the case; the algorithm will simply fail to find a solution and terminate after a user-specifiable number of iterations.
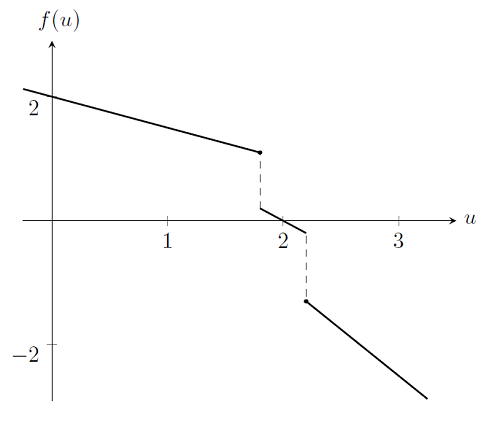
Case 3: The Problem Is Non-Smooth and Non-Differentiable
Last, consider the case of a material property that has a discontinuous change in properties. For example, consider the same system as before, but with a spring stiffness that has different values over different intervals, a value of k=0.5 for u\le1.8, a value of k=1 for 1.8<u<2.2, and k=1.5 for u\ge2.2. If we plot out f(u) for this case we see that it is non-differentiable and discontinuous, which is a violation of the requirements of the Newton-Raphson method. It is also clear by examination that unless we choose a starting point in the interval 1.8<u<2.2 the Newton-Raphson iterations will oscillate between iterations outside of this interval.
To summarize, so far we have introduced the damped Newton-Raphson method used to solve nonlinear finite element problems and discussed the convergence criteria used. We introduced several ways in which this method can fail to find a solution, including:
- Choosing an initial condition that is too far away from the solution
- Setting up a problem that does not have a solution
- Defining a problem that is non-smooth and non-differentiable
Interpreting the COMSOL Log File
The Log File
We will soon discuss ways of addressing all of these issues, but first, let’s take a look at the log file of a typical nonlinear finite element problem. Below you will see the log file (with line numbers added) from a geometric nonlinear structural mechanics problem:
1) Stationary Solver 1 in Solver 1 started at 10-Jul-2013 15:23:07. 2) Nonlinear solver 3) Number of degrees of freedom solved for: 2002. 4) Symmetric matrices found. 5) Scales for dependent variables: 6) Displacement field (Material) (mod1.u): 1 7) Iter ErrEst Damping Stepsize #Res #Jac #Sol 8) 1 6.1 0.1112155 7 3 1 3 9) 2 0.12 0.6051934 1.2 4 2 5 10) 3 0.045 1.0000000 0.18 5 3 7 11) 4 0.012 1.0000000 0.075 6 4 9 12) 5 0.0012 1.0000000 0.018 7 5 11 13) 6 1.6e-005 1.0000000 0.0015 8 6 13 14) Stationary Solver 1 in Solver 1: Solution time: 1 s 15) Physical memory: 849 MB 16) Virtual memory: 946 MB
Explanations
- Line 1 reports the type of solver called and the start time.
- Line 2 reports that the software is calling the nonlinear system solver.
- Line 3 reports the size of the problem in terms of the number of degrees of freedom.
- Line 4 reports on the type of finite element matrix to be solved.
- Lines 5-6 report the scaling. In this case, the displacement field scale is 1 m, which is appropriate for the expected magnitude of the solution.
- Lines 7-13 report that six Newton-Raphson iterations were used to arrive at the converged solution. The first column reports the iteration number and the second reports the error estimate used to define convergence. By default, the convergence criterion is 0.001. The third column shows that some damping was used for the first two steps, but steps 3-6 were undamped.
- Lines 14-16 report the solution time and memory requirements.
Now you should have gained an understanding of how nonlinear static problems are solved in COMSOL as well as how to interpret the log file.




Comments (8)
Joseph O'Day
November 19, 2013I really appreciate this post–more nonlinear solving explanations please!
Terry Lou
March 24, 2014Very informative post Walter especially about the possible reasons for non-converged solution. I would like to expand this discussion a little further on “divergence” of the solution which is a kind of error leads to the no converged solution. The common information for this kind of error is
“Failed to find a solution.
Divergence of the linear iterations.
Very ill-conditioned preconditioner.
The relative residual is more than 1000 times larger than the relative tolerance.
Returned solution is not converged.”
I would appreciate if you can make some comment on possible reasons lead to divergence error. Thanks again for the wonderful post.
Terry
Walter Frei
March 27, 2014Dear Terry,
This is usually a symptom of a problem which is not constrained. Try solving a 3D problem using an iterative solver, and apply a load, but not constraints, you’ll often get this type of error. Also, continue reading the solver series of blogs for more details: http://www.comsol.com/blogs/tag/solver-series/
Yalcin Kaymak
April 11, 2014There is also a third case. Consider the function f(u)=1-u^(1/3). There is a solution at u=1, but the above mentioned iterations cannot find it. Actually the problem is smooth and differentiable. But its differential is not smooth and continuous at solution 🙂
Walter Frei
April 11, 2014Dear Yalcin, There are certainly some mathematically interesting “corner cases” such as this, and others, that you will come across for problems with only a single unknown. In practice these cases are less relevant for the types of nonlinearities that are faced in nonlinear and multiphysics finite element modeling. You’ll find that the techniques of load ramping and nonlinearity ramping discussed in later blogs here are sufficient for addressing stationary problems. There are, however, cases where a great deal of physical insight about the problem is needed. For a good example, please see: http://www.comsol.com/model/postbuckling-analysis-of-a-hinged-cylindrical-shell-10257
Ting Lau
March 7, 2015HI,
The explanation for the log file is very helpful, understanding the step and the error and time step etc.
But, I still do not understand is what is the #Res #Jac #Sol?
I read the reference manual that Res is the number of residuals and Jacobians and liner system solutions.
But, what does it means ?
Thank you again for the post.
Ting
Walter Frei
March 9, 2015Dear Ting,
Although the solver log does give a great deal of information, most of it is actually not required for you to get a converged model. Please continue reading this blog series on solver settings, and you will understand the general approach that will lead to convergence (when physically possible.) These level of solver log details are, in practice, essentially unnecessary for practical usage of the software. If you do want to understand them, I suggest a more careful reading of the documentation and the supporting references.
Akash Meena
April 9, 2020So, what is the solution of
Case 3: The Problem Is Non-Smooth and Non-Differentiable ?
If its non smooth and discontinuous, how can I alter this graph ?
Thank you.